Please spend a few minutes reviewing the 3 documents below.
Chapter 31 - Real Estate Math
Learning Objectives
At the completion of this chapter, students will be able to do the following:
1) Explain how to calculate a broker’s commission on a transaction.
2) Explain the two qualification ratios used by lenders during the underwriting process.
31.1 Introduction to Real Estate Math
Transcript
In this chapter, we will cover the various types of real estate math related questions you need to know as a real estate salesperson. Some students get nervous about having to solve math problems, but rest assured, it’s not as difficult as you may think. Real estate math mainly involves basic addition, subtraction, multiplication, and division. You simply have to follow the formulas we will provide to you. In addition, you can use a calculator to do much of the heavy lifting.
In the next lesson, we will give you a PDF ‘cheat sheet’ that shows all of the formulas you need to know. We recommend that you download the PDF and use it as a study aid for both the final exam as well as the State exam.
The following lessons will cover area calculations, commission calculations, simple interest and mortgage calculations, loan origination fees and discount points, loan to value ratios, qualification ratios, and finally appreciation and depreciation. These topics will cover much of what you need to know to solve any math related problems you may encounter in your day-to-day practice as a real estate salesperson.
That being said, let’s jump right in!
Key Terms
31.2 Real Estate Formulas

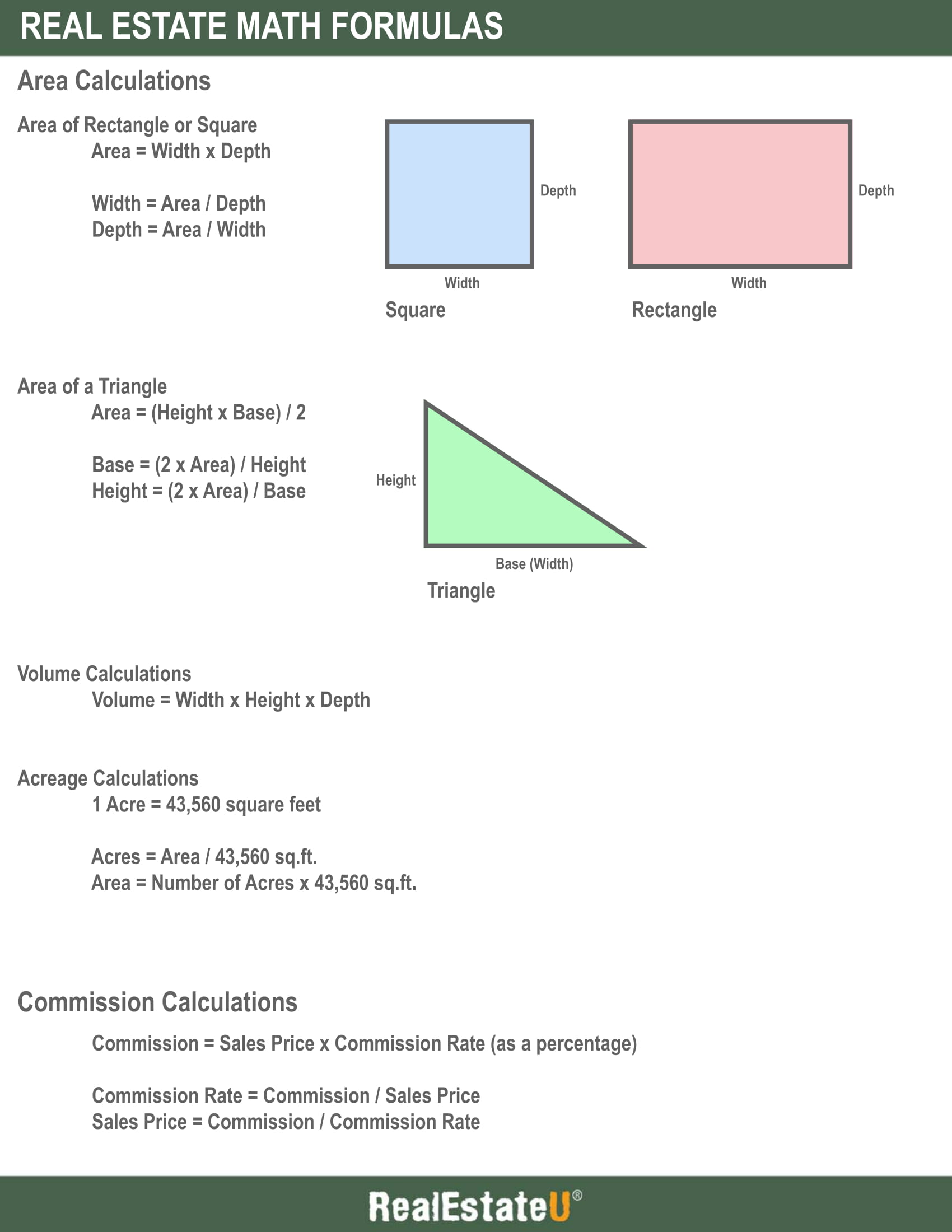

31.3 Area Calculations
Transcript
In this lesson, we will cover some of the most commonly used area calculations in real estate. These calculations will be used in your day-to-day practice as a real estate salesperson.
Let’s start by going over the area of squares and rectangles.
The formula for the area of a square or rectangle is the same.
It equals the following:
Area = Width x Depth
Let’s go through a quick example to see how to use this formula.
We’ll assume a house measures 20’-0” (twenty feet) wide by 40’-0” (forty feet) deep. What is the area of the house?
Since the area equals width times depth, we simply multiply 20’-0” by 40’-0” to get a total area of 800 square feet.
When you input the known numbers into the formula, you get the following:
Area = 20’-0” (width) x 40’-0” (depth)
Area = 800 square feet
You can take the formula for area one step further. If the area and either the width or depth is known, you can solve for the remaining unknown dimension. The formulas will equal the following:
Width = Area / Depth (Area divided by Depth)
Depth = Area / Width (Area divided by Width)
For example, if a one-story house totals 1,500 square feet in area with a width of 30’-0” (thirty feet), what is the depth of the house?
Since we know the area and the width, we use the formula:
Depth equals the area divided by the width.
1,500 square feet divided by 30’-0” equals a depth of 50’-0” (fifty feet).
Next, we’ll cover how to calculate the area of a triangle.
The formula for the area of a triangle equals:
Area = (Height x Base) / 2
The base is also known as the width.
You can think of a triangle as one-half a rectangle, divided diagonally through the center. This is why you can take the area of a rectangle and divide it by two to get the area of a triangle, if the base and width dimensions were the same.
Let’s go through an example.
We’ll assume a triangle measures 12’-0” wide by 4’-0” high. What is the area of the triangle?
The first thing we need to do is multiply the base dimension by the width. This equals 12’-0” times 4’-0”, or 48 square feet.
Next, we divide 48 square feet by 2 to get 24 square feet. This is the area of the triangle.
If you already know the height and area of a triangle, you can solve for the base dimension using the following formula:
Base = (2 x Area) / Height
For example, if a triangle measures 10’-0” (ten feet) high with an area of 120 square feet, what is the base dimension?
Using the formula, we first multiply the area by 2. This equals 120 square feet times 2, or 240 square feet.
Next, we divide 240 square feet by the height of 10’-0” to get a base dimension of 24’-0”.
Similarly, if the area and base dimension of a triangle is known, you can solve for the height using the following formula:
Height = (2 x Area) / Base
Questions using this formula can follow the same two steps we just did when solving for the base dimension.
Next, we’ll cover how to convert square footage into acres.
It’s important to note that 1 Acre equals 43,560 square feet. Please memorize this number as it will appear on your final and state exams.
Anytime you have to convert acres into square footage, you must use the following formula:
Acres = Area / 43,560 S.F.
For example, how many acres is 196,020 square feet?
Using the formula, we must divide 196,020 by 43,560 to get an answer of 4.5 acres.
You can also use a variation of this formula to solve for the total number of square feet, if the number of acres is known. The formula will equal:
Square Feet = Number of Acres x 43,560 S.F.
Let’s go through a quick example.
If a property totals 0.80 acres, how many square feet is the property?
Using the formula, we must multiply the known acreage by 43,560.
This equals 0.80 times 43,560, or 34,848 square feet.
Next, we’ll cover how to solve problems involving perimeter measurements.
The formula to determine the perimeter dimension is:
Perimeter = Sum of all sides of an object
For example, a homeowner has a property that measures 50’-0” (fifty feet) by 120’-0” (one hundred and twenty feet). If the homeowner builds a fence around the entire perimeter of the property, what is the total length of the fence?
To solve this problem, we simply have to add up the four sides. Two of the sides will equal 50’-0” and the other two sides will equal 120’-0”.
50’-0” + 50’-0” + 120’-0” + 120’-0” = 340’-0”
In the last section of this lesson, we will cover how to calculate volume.
The formula for volume equals the following:
Volume = Width x Height x Depth
For example, what is the volume of a house that measures 25’-0” x 30’-0” x 30’-0”?
Using the formula, we simply multiply the three dimensions together.
This equals 25’-0” x 30’-0” x 30’-0”, or 22,500 cubic feet.
Key Terms
31.4 Commission Calculations
Transcript
Real estate brokers are paid a commission as compensation. The commission earned is usually based on a percentage of the sales price, not the listing price. For this reason, it is important to understand how to calculate commissions earned on a transaction.
Before we get started, it is important to note that there is no standard commission rate, as the commission is always negotiated between the seller and the listing broker. The commission will be documented in the listing agreement.
Let’s start by going through an example.
A property is listed for $656,000 with a negotiated commission of 5%. If the property eventually sells for $630,000, how much is paid in commissions?
Remember, commissions are based on the sales price, not the listing price, which means we apply the 5% commission rate to $630,000.
The first step we must take is to convert the commission rate to a decimal. 5% expressed as a decimal is 0.05.
Next, we multiply 0.05 by the sales price of $630,000 to get a total commission of $31,500.
If no other broker was involved in the transaction, the listing broker will get to keep the full $31,500. This means the listing broker was responsible for finding a buyer, and the buyer was not represented by another broker. However, this is usually not the case. In most transactions, the listing broker will split the total commissions paid by the seller with the buyer’s broker and any salespersons working under them on the deal.
Let’s go through a scenario where the buyer is represented by a broker and the listing broker agrees to split their commission.
If the buyer is represented by another broker, the listing broker and buyer’s broker must negotiate how the commission will be split between the two. Typically, the commission is split 50/50, but it may also be 60/40, 70/30, etc. It all depends on what the two parties agree upon.
For example, let’s assume a property sells for $390,000 with a total commission of 6%. If the listing broker and buyer’s broker agree to split the commission 50/50, how much will the buyer’s broker earn as a commission?
The first step we take is to convert the commission rate to a decimal. 6% expressed as a decimal equals 0.06.
Next, we determine the total commission in the deal. This equals 0.06 multiplied by the sales price of $390,000. $390,000 times 0.06 equals $23,400.
Finally, we determine the buyer’s broker commission on the deal. Since the two brokers agree to split the commission 50/50, we simply divide the total commission paid by 2. This equals $23,400 divided by 2, or $11,700.
The listing broker will also earn a commission of $11,700.
Let’s go through one more example using this scenario.
We’ll assume a condo sells for $520,000 with a 4% commission rate. The listing broker and buyer’s broker agree to split the commission 60/40 (60% going to the listing broker and 40% going to the buyer’s broker). How much will each broker earn in the transaction?
Like before, the first step is to convert the commission rate to a decimal. 4% as a decimal equals 0.04.
Next, we determine the total commission paid. This equals 0.04 times the sales price of $520,000, or $20,800.
Next, we determine how much the listing broker will earn by multiplying the total commission by 0.60, or 60%. This equals $20,800 times 0.60, or $12,480.
Finally, we determine the buyer’s broker’s commission by multiplying the total commission by 0.40, or 40%. This equals $20,800 times 0.40, or $8,320.
We can take this a step further by including commission splits between the listing or buyer’s broker and their salespersons. This is a more common scenario and will directly apply to you as a salesperson. Since the law requires you to work under a sponsoring broker, any commission you earn must be paid to you by your broker, not the seller.
In this scenario, the seller will pay the full commission to the listing broker. The listing broker will then pay the buyer’s broker an agreed upon percentage of the total commission (50% for example). The listing and buyer’s broker will then split their portion of the commission with the salesperson working under them on the transaction. The commission split between a real estate salesperson and their sponsoring broker is also negotiable and will be spelled out in the independent contractor agreement.
Let’s go through an example to see how this all works.
We’ll assume a house just closed for $380,000. The seller agreed to pay a 6% commission. The listing broker and the buyer’s broker agreed to split the commission 50/50. If the listing broker had a salesperson in their office work on the day-to-day details of the transaction, how much will the listing broker’s salesperson make if they agreed to split the commission 50/50?
As before, we must first convert 6% to a decimal, which equals 0.06.
Next, we determine the total commission. This will equal 0.06 times the sales price of $380,000, or $22,800.
Next, we determine the listing broker’s commission. Since the listing broker and buyer’s broker agree to split the total commission 50/50, we must divide the total commission paid by 2. This equals $22,800 divided by 2, or $11,400.
Finally, we determine the salesperson’s commission. Since the salesperson and listing broker also agreed to a 50/50 split, the salesperson will get half of what the listing broker earned on the deal. This equals $11,400 divided by 2, or $5,700.
Let’s go through one last example, this time a bit more complicated.
John is a real estate salesperson working under the listing broker on a deal. The seller agreed to pay a 5% commission, and John’s broker agreed to split the commission 60/40 with the buyer’s broker (60% going to the listing broker and 40% going to the buyer’s broker). John and his sponsoring broker agreed to split the commission 40/60 (40% going to John and 60% going to his broker). How much will John make as a commission if the property sells for $430,000?
Let’s follow the same steps as before, starting with converting the commission rate to a decimal. 5% expressed as a decimal is 0.05.
Next, we determine the total commission paid on the transaction. This equals $430,000 times 0.05, or $21,500.
Next, we determine the listing broker’s commission. Since the listing broker will earn 60% of the total commission, we must multiply the commission by 0.60. This equals $21,500 times 0.60, or $12,900.
Finally, we determine John’s commission. Since John will earn 40% of his broker’s commission, John will earn $12,900 times 0.40, or $5,160.
We can follow the same steps to determine the commission earned by the buyer’s broker’s salesperson working on the transaction.
The buyer’s broker will earn 40% of the total commission. This equals $21,500 times 0.40, or $8,600. If the buyer’s broker and their salesperson agreed to split the commission 50/50, the salesperson will earn half of their broker’s commission. This will equal $8,600 divided by 2, or $4,300.
And there you have it! These are the commission scenarios you will encounter on nearly all of your transactions. As mentioned at the start of this lesson, it’s very important to fully understand how commissions are calculated.
Key Terms
31.5 Simple Interest and Mortgage Calculations
Transcript
In this lesson, we will cover how to calculate interest on a loan and mortgage payment.
We’ll start with interest-only loans, also known as term loans, as they are much simpler to calculate compared to amortizing loans.
As the name suggests, interest-only loans only include interest payments, which means the principal balance of the loan always stays the same. The borrower will have to repay the full loan amount at the end of the loan term, also known as a balloon payment.
We can use the following formula to determine how much is paid in interest each year:
Yearly Interest Payment = Loan Amount x Interest Rate
Let’s go through a quick example to see how this formula works.
David obtained a $650,000 interest-only loan at a 6% interest rate. How much will David pay in interest each year?
The first step we must take is to convert the interest rate to a decimal. 6% expressed as a decimal equals 0.06.
Next, we multiply 0.06 by the loan amount. This equals 0.06 times $650,000, which gives us $39,000.
David will pay $39,000 in interest each year.
However, most loans are paid on a monthly basis. To determine the monthly payment on the loan, we simply divided the yearly interest paid by 12 months. This equals $39,000 divided by 12, or $3,250.
Let’s go through one more example.
What is the monthly payment on a $520,000 interest-only loan with an interest rate of 5.25%?
First, we convert 5.25% to a decimal. This equals 0.0525.
Second, we calculate the yearly interest by multiplying 0.0525 by the loan amount. This equals 0.0525 times $520,000, or $27,300.
Finally, we divide the yearly interest by 12 months, which equals $27,300 divided by 12, or $2,275.
Now that we know how to calculate simple interest on an interest-only loan, let’s go over how to calculate monthly mortgage payments on fully amortizing loans. Unlike an interest-only loan, a fully amortizing loan payment includes both principal and interest. Each month, the amount of principal being paid off gradually increases, while the amount of interest paid gradually decreases; however, the monthly loan payment remains the same.
In order to accurately determine the monthly payment on a fully amortizing loan, you must know the loan amount, the term of the loan and the interest rate. But even then, you still need a mortgage calculator to run the calculation. As an alternative, you can use a mortgage payment table, which gives you a factor that applies to each $1,000 of the loan amount. To find a mortgage payment table, simply Google the term to find several examples. The numbers on the table are constant, so any example you find will be sufficient.
The mortgage payment table includes a series of interest rates at 1/8% intervals and a factor number for both 15-year loans and 30-year loans. For example, the factor for a 30-year loan at 4.125% interest is 4.84. Or, the factor for a 15-year loan at 5.875% interest is 8.37.
But how do we use the factor to determine the monthly payment on a loan?
There are three simple steps you need to follow:
- Step 1: get the factor from the mortgage payment table.
- Step 2: divide the loan amount by $1,000.
- Step 3: multiply the factor by the number obtained in step 2.
Let’s go through an example using these steps.
We’ll assume the loan amount is $560,000, with a 30-year term and a 3.875% interest rate. What is the monthly loan payment?
First, we get the factor. By scanning through the table we see the factor for a 30-year loan at 3.875% interest is 4.70.
Next, we divide the loan amount by $1,000. This equals $560,000 divided by $1,000, or $560.
Finally, we multiply the factor of 4.70 by $560 to get a monthly loan payment of $2,632. This is the amount of principal and interest paid each month on the loan.
Let’s go through one more example using the factor.
John is obtaining a $320,000 mortgage, with a 15-year term at 4.5% interest. How much will John pay each month in principal and interest?
First, we obtain the factor for the 15-year loan at 4.5% interest. By looking at the table, we can see the factor is 7.64.
Next, we’ll divide the loan amount by $1,000. This equals $320,000 divided by $1,000, to get $320.
Finally, we multiply the factor of 7.64 by $320 to get a monthly loan payment of $2,444.80.
Using the mortgage payment table is a great way to quickly calculate the monthly payment on a loan if you do not have a mortgage calculator available.
Key Terms
31.6 Loan Origination Fees and Discount Points
Transcript
In this lesson, we will go over how to calculate two fees associated with the loan origination process. These are fees paid upfront by the borrower to the lender, prior to closing on the loan.
Let’s start by going over loan origination fees. The processing of a loan is known as loan origination. The loan origination fee is charged by the lender (and paid by the borrower) to cover the expenses involved in creating a new loan. Loan origination fees vary per lender and may be negotiated between the lender and borrower. A typical loan origination fee is 1% of the loan amount (NOT the purchase price).
Let’s go through an example to see how a loan origination fee is calculated.
John is purchasing a $680,000 house and needs to obtain a $550,000 loan to close on the property. How much will John pay as a loan origination fee if the lender charges a fee of 1%?
The first step we must take is to convert 1% to a decimal. This equals 0.01.
Next, we must multiply 0.01 by the loan amount. Remember, loan origination fees are based on the loan amount, not the purchase price. This equals 0.01 times $550,000, or $5,500.
John will pay a loan origination fee of $5,500 to the lender.
Let’s go through one more example.
Abby is looking to obtain a $320,000 loan to purchase a $500,000 house. The lender initially wanted to charge a 1% loan origination fee; however, Abby was able to negotiate the fee down to 0.5%. How much will Abby pay in loan origination fees?
In this case, the fee is based on 0.5%. Remember, loan origination fees may be negotiated with the lender. When we convert 0.5% to a decimal, we get 0.005.
Next, we multiply 0.005 by the loan amount of $500,000, which gives us a loan origination fee of $1,600.
We can also solve for the loan amount or the loan origination fee percentage if we know the other two variables. If we know the loan origination fee percentage and the amount paid in origination fees, we can solve for the loan amount. This will equal:
Loan Amount = Amount Paid in Origination Fees / Loan Origination Fee Percentage (expressed as a decimal.
For example, if a borrower paid $1,500 in origination fees and the lender charges a 1% fee, how much is the loan amount?
To find the answer, we simply divide $1,500 by 0.01 (which is 1% expressed as a decimal). This gives us a loan amount of $150,000.
Now, if we know the loan amount and the amount paid in origination fees, we can solve for the fee percentage.
Loan Origination Fee Percentage = Amount Paid in Origination Fees / Loan Amount.
For example, if a borrower obtained a $200,000 loan and paid $1,000 in origination fees, what was the lender’s origination fee?
To solve this, we simply divide $1,000 by $200,000, to get a fee of 0.5%.
These are the three types of questions you may see regarding loan origination fees.
Now let’s turn to discount points.
Discount points, also known as mortgage points, is a fee paid to the lender (by the borrower) at closing in exchange for a reduced interest rate.
For example, a borrower may pay 1 discount point upfront in exchange for a reduced interest rate of 0.25%. The amount of reduction in interest rate per discount points paid depends on the lender’s projected yield on the loan. The lender has to calculate how much they can accept upfront in exchange for less money collected each month, and still reach their desired return on investment.
The borrower does not have to opt-in to paying discount points, but doing so will reduce their monthly loan payments since their interest rate will be lowered.
Like loan origination fees, discount points are paid as a percentage of the loan amount.
1 discount point is equal to 1% of the loan amount.
For example, if a borrower elects to pay 2-1/2 points upfront, this means they will pay a fee of 2.5% of the loan amount.
The formula you can use to solve these types of problems is:
Amount Paid in Discount Points = Loan Amount x Discount Points (expressed as a decimal)
Let’s go through an example using this formula.
Mark is looking to borrow $250,000 to purchase a $400,000 house. The loan has a 30-year term with an interest rate of 4.5%. Mark learns that he has the option to pay 1 point upfront, which will reduce his interest rate to 4.25%. How much will Mark pay in discount points if he elects to take this option?
The first step we have to take is to determine what percentage of the loan amount is paid in discount points and convert that number to a decimal. 1 point is equal to 1% of the loan amount, which equals 0.01 as a decimal.
Next, we now know that discount points are based on the loan amount, rather than the purchase price. This means we must multiply 0.01 by the loan amount of $250,000, to get an answer of $2,500. In other words, Mark will pay the lender $2,500 upfront to reduce his interest rate from 4.5% to 4.25%.
If you know the amount paid in discount points and the loan amount, you can use a variation of the formula to solve for the number of points. This variation will look like the following:
Discount Points = Amount Paid in Discount Points / Loan Amount
Let’s go through an example using this variation.
We’ll assume the borrower is paying $9,500 in discount points upfront. If the loan amount is $380,000, how many discount points did the borrower pay?
To find the answer, we simply divide the amount paid in points by the loan amount. This equals $9,500 divided by $380,000, or 0.025. 0.025 expressed as a percentage equals 2.5%, which amounts to 2.5 points.
Finally, we can do one more variation on the formula and solve for the loan amount if we know the number of discount points and the amount paid in discount points. The variation will equal the following:
Loan Amount = Amount Paid in Discount Points / Number of Discount Points
For example, if a borrower paid $10,000 upfront for 2 discount points, what was the loan amount?
First, we must convert 2 discount points to a decimal. This equals 0.02.
Next, we divide $10,000 by 0.02. This will give us a loan amount of $500,000.
These are the three types of questions you may see regarding discount points.
Key Terms
31.7 Loan to Value Ratio
Transcript
In this lesson, we will review the loan to value ratio, which is used by lenders to help determine the maximum loan amount on a property.
The loan to value ratio (also known as LTV) is the ratio of debt to the value of the property.
It is important to note that the value used in the LTV calculation is based on the sales price/contract price, or the appraised value, whichever is LESS. Lenders use the lesser of the two values to help reduce their risk on the loan.
The formula for LTV reads as such:
LTV = Loan Amount divided by Value of Property (Loan Amount / Value of Property)
What this formula shows us is that the higher the LTV, the lower the down payment, and visa-versa.
Let’s go over a few examples to help illustrate how LTV is used in a residential transaction.
Example 1:
Amber is looking to obtain a loan to purchase a new house. The contract price is $410,000, but the property was appraised for $425,000. What is the LTV if the lender agrees to give Amber a $328,000 loan?
Since LTV equals the loan amount divided by the value of the property, and the lender will use the lesser of the two values, we can use the following formula:
LTV = $328,000 / $410,000 = 0.80 or 80%
Example 2:
A property is under contract for $520,000, but the appraisal came back at only $490,000. What is the maximum loan amount a lender will provide using a 70% LTV?
Once again, we have to use the lesser of the two values. Since the appraisal came in lower than the contract price, we must apply the LTV to $490,000.
To find the answer, we simply multiply 70% (which is the LTV) by $490,000:
$490,000 x 0.70 = $343,000
Example 3:
A lender is offering a buyer a loan with an LTV of 85%. Assuming the contract price and appraised value are equal, what is the value of the property if the loan amounts to $280,500?
To find the answer, we must divide the loan amount by the LTV:
$280,500 / 0.85 = $330,000
We can check the answer by simply multiplying the LTV by the value:
$330,000 x 0.80 = $280,500
Let’s now use the LTV formula to determine the down payment on a property.
Example 4:
Justin is looking to purchase a property for $260,000. The appraisal came back at $265,000. If the lender is willing to offer a 75% LTV, how much of a down payment is required by Justin?
Step 1: determine the maximum loan amount.
To find the loan amount, simply multiply the lesser of the two values by the LTV.
This equals $260,000 x 0.75 = $195,000
Step 2: subtract the loan amount from the contract price.
$260,000 - $195,000 = $65,000
Key Takeaways
- Remember to always use the lesser of the sales price or appraised value.
- The higher the LTV, the lower the down payment.
Key Terms
31.8 Qualification Ratios
Transcript
During the underwriting process, the underwriter uses two ratios to help determine if a borrower will qualify for a loan.
These two ratios are known as the housing expense ratio and the debt-to-income ratio.
The housing expense ratio is also referred to as the front-end ratio, while the debt-to-income ratio is known as the back-end ratio.
For the purposes of this lesson, we will use the ratios set forth by the FHA; however, every lender may use slightly different qualifying ratios.
The housing expense ratio
The FHA currently sets the housing expense ratio at 31%.
This only takes into account housing-related expenses, such as monthly mortgage payments, property taxes, insurance, etc.
The formula for the housing expense ratio equals the following:
Total Monthly Housing Expenses divided by Total Monthly Income (Total Monthly Housing Expenses / Total Monthly Income)
What this ratio means is a borrower’s total monthly housing expenses cannot exceed 31% of their gross monthly income.
Let’s take a look at an example to illustrate how this ratio is used.
Amy is looking to obtain a $265,000 loan to purchase a $410,000 house. Amy’s monthly housing expenses amount to the following:
Mortgage payment: $1304
Property taxes: $380
Insurance: $95
Will Amy qualify for the loan if her monthly income equals $5,800?
To answer this question, we first have to add up the total housing costs. These equal:
$1,304 + $380 + $95 = $1,779
Next, we have to divide this number into Amy’s monthly gross income:
$1,779 / $5,800 = 0.3067 or just under 31%.
In this example, Amy would qualify on the front-end ratio because her housing expenses do not exceed 31% of her monthly income.
Next, Amy will also have to qualify using the back-end ratio.
Debt-to-income ratio
The FHA currently sets the debt-to-income ratio at 43%.
The debt-to-income ratio takes into account all of the borrower’s monthly recurring financial obligations in relation to their monthly income. In other words, what other loans is the borrower responsible for?
These include all housing expenses from the front-end ratio plus any outstanding student loans, car loans, credit cards, phone loan, etc.
All of the borrower’s recurring monthly obligations cannot exceed 43% of their monthly income.
Let’s continue with the previous example to see if Amy will qualify on the back-end ratio.
Amy’s monthly housing expenses total $1,779.
In addition, Amy has the following monthly loan bills:
Student loans: $350
Car loan: $410
Credit cards: $90
Smartphone: $45
These debt obligations add up to $895.
When we add Amy’s housing expenses to her other debt obligations, we get a total of $2,674 ($1,779 + $895).
Finally, we have to divide $2,674 into her gross monthly income of $5,800.
$2,674 / $5,800 = .461 or 46%.
Since Amy’s back-end ratio exceeds 43%, she will not qualify for the loan.
In order to qualify, she will have to pay off some of her existing debt to lower her monthly debt obligations.
For example, if Amy were to pay off her student loans, her back-end ratio would drop to 40% and thus allow her to qualify for the new mortgage.
Key Terms
31.9 Appreciation and Depreciation
Transcript
In this lesson, we will cover the concepts of appreciation and depreciation and how to calculate them.
Appreciation refers to an increase in value. Appreciation is expressed as a percentage increase in value over a period of time.
The formula for appreciation is the following:
Value of the Property x 1 plus the amount of appreciation expressed as a decimal.
Since the value of the property is increasing in value, we must add 1 to the amount of appreciation.
For example, if a property appreciated 3% in the past year, how much would the property be worth today if it was valued at $100,000 a year ago?
Let’s apply the formula for appreciation to find the answer.
The property was worth $100,000 and increased 3% in value.
First, we convert 3% to a decimal, which equals 0.03.
Next, we add 1 to get 1.03.
Finally, we multiply 1.03 by $100,000 to get $103,000.
This means the property appreciated $3,000 in one year.
But what if we want to calculate the appreciated value over several years, rather than just one year?
To find this we use the following steps:
First, convert the amount of appreciation to a decimal.
It’s important to note that the rate of appreciation must be constant when using this formula.
Second, add 1.
Third, raise 1 plus the percentage of appreciation to the number of years the appreciation occurs.
Lastly, multiply the raised number by the original value of the property.
Let’s go through an example to see how this works.
A property is valued at $240,000. The homeowner expects the property to appreciate at 2.5% over each of the next 4 years. What is the value of the property after 4 years?
First, convert 2.5% to a decimal. This equals 0.025.
Second, add 1. This equals 1.025.
Third, raise 1.025 to the 4th power. This gets us 1.1038.
Finally, we multiply 1.1038 by $240,000 to get $264,912.
This means the property appreciated $24,912 in value over 4 years.
Another way to solve an appreciation problem is to multiply the amount of appreciation each year by the value of the property from the previous year.
For example, a property is currently worth $320,000. After one year, the property will appreciate 2%, followed by 3% in the next year, followed by 1.5% in the third year. What is the value of the property after year three?
To solve this problem, we convert the first year’s appreciation of 2% to a decimal and add 1. This equals 1.02. Then, we multiply the value of the property by 1.02, which gives us $326,400. This is the value after year one.
Next, we multiply $326,400 by the amount of appreciation in year two. This equals $326,400 times 1.03 (since there is a 3% rate of appreciation), which gives us a value of $336,192. This is the value of the property after year two.
Finally, we multiply $336,192 by 1.015 (or a 1.5% rate of appreciation) to get a value of $341,234.88 after year three.
Now that we covered appreciation, let’s move on to depreciation. Depreciation is the loss in value over time, which is also expressed as a percentage of value. The formula for depreciation equals the following:
Value of the Property x (1 – Rate of Depreciation)
Let’s go through an example to see how this formula works.
Let’s assume a property is currently worth $280,000. How much will the property be worth after one year if it depreciates by 4%?
The first step we need to do is subtract 4% from 1. This equals 1 minus 0.04, or 0.96.
The second step is to multiply 0.96 by the current value, which equals $268,800. This means the property lost $11,200 in value in one year.
If the rate of depreciation is constant over a period of time, we can take the following steps to find the total loss in value.
First, subtract the rate of depreciation (expressed as a decimal) from 1.
Second, raise that number to the number of years of depreciation.
Finally, multiply by the starting value of the property.
Let’s go through a scenario to see how this works.
We’ll assume a property is worth $160,000. The property will depreciate by 3.5% over each of the next 5 years. What is the value of the property after 5 years?
The first step is to subtract 3.5% from 1, which equals 0.965.
Next, we raise 0.965 to the 5th power. This equals 0.8368.
Finally, we multiply this number by the original value of the property:
$160,000 x 0.8368 = $133,888.
Just like we learned with appreciation, you can calculate the rate of depreciation per year to arrive at the final value.
For example, a property is worth $590,000. The property will depreciate 3.5% in year one, 2.5% in year two and 1.8% in year three. What is the value of the property after three years?
First, we’ll determine the value of the property after year one. This equals 1 minus 3.5%, or 0.965, multiplied by $590,000, which gives us a value of $569,350.
Next, we take this value and multiply it by 1 minus 2.5%, or 0.975. $569,350 times 0.975 equals $555,116.25. This is the value of the property after two years.
The last step is to multiply $555,116.25 by 1 minus 1.8%, or 0.982. $555,116.25 times 0.092 equals $545,124.16. This is the value after three years.
In the real world, properties appreciate and depreciate in value all the time. One year, the value may go up, followed by several years of depreciation. It all depends on the market conditions surrounding the property.
Let’s take the concept of appreciation and depreciation one step forward and calculate the final value of a property that appreciates and depreciates over time.
We’ll assume the property is currently worth $640,000. The property will appreciate by 2% in year one, followed by 3% of depreciation in year two and 4% of appreciation in year three. What is the value of the property after three years?
We’ll solve this problem by taking it one year at a time. Since the property will increase in value in year one, we must add 1 to 2% and multiply by the value of the property. This equals 1.02 times $640,000, or $652,800.
The value in year two will decrease, which means we must multiply the year one value of $652,800 by 1 minus 3%. This equals $652,800 times 0.97, or $633,216.
Finally, in year three, the property will increase in value by 4%. This means we multiply the year two value of $633,216 by 1 plus 4%. This gives us a year three value of $633,216 times 1.04, or $658,544.64.
These are the various ways to calculate appreciation and depreciation.
Key Terms
COPYRIGHTED CONTENT:
This content is owned by Real Estate U Online LLC. Commercial reproduction, distribution or transmission of any part or parts of this content or any information contained therein by any means whatsoever without the prior written permission of the Real Estate U Online LLC is not permitted.
RealEstateU® is a registered trademark owned exclusively by Real Estate U Online LLC in the United States and other jurisdictions.